语义信息G理论研究进展

鲁晨光^1，2

1 辽宁工程技术大学数学和人工智能学院，中国阜新

2 长沙学院计算机工程和应用数学学院，中国长沙

摘  要：作者32年前推广香农信息论得到语义信息G理论(G表示推广，G理论也曾叫“广义信息论”)。G理论的核心思想是：1)使用P-T概率框架和表示语义的真值函数；2)用真值和逻辑概率之比的对数(负的正则化失真)定义语义信息测度；3)把信息率失真函数推广为信息率逼真函数; 4)结合投资组合定义信息价值。最近十年，作者把G理论应用于机器学习，提出语义信道和香农信道相互匹配的一组算法——用于多标签学习，最大互信息分类，混合模型，求解隐含变量，贝叶斯确证，约束控制(或主动推断)等领域。作者发现变分贝叶斯(VB)和最小自由能原理(FEP)存在反例和局限性(只用似然函数作为约束条件)，最近提出语义变分贝叶斯(SVB)和最大信息效率原理(MIEP)。SVB比VB计算更简单也更易于理解，MIEP比FEP更易于理解、更和物理学自由能概念兼容、用来解释生物自组织也更方便。G理论有待结合深度学习方法进一步发展。

关键字：语义信息论，机器学习，变分贝叶斯，最小自由能原理，最大信息效率原理 。

                                                                     作者简介

鲁晨光,男,1955年8月生,曾任长沙大学计算机系副教授,长沙青年学术带头人。  曾在加拿大尼亚加纳学院接受培训并在北师大数学系做访问学者。现为辽宁工程技术  大学客座教授。主要研究兴趣是:语义信息论、机器学习、色觉机制、投资组合、美感和进化。提出色觉机制的译码模型和广义信息论(即语义信息论)。于《通信学报》、《光学学报》、Int. J. of General Systems, Entropy、Information等国内外期刊发表约40篇论文;出版学术专著4部。Email:lcguang@foxmail.com.个人主页:http://survivor99.com

    一. 引  言

Weaver在香农发表著名论文不久就提出语义信息研究【1】。关于语义信息的理论有多种，在我之前有Carnap和Bar-Hillel提出的语义信息论【2】，Dretske 的知识与信息理论【3】，钟义信教授提出的语义信息论【4】。我于1993年发表专著《广义信息论》【5】。在我之后有Floridi提出的强语义信息论【6】以及其他人提出的语义信息论或相关理论【7,8】。

在我提出的语义信息论中，语义信息测度是香农信息测度的自然推广， 信息率逼真函数R(G)是信息率失真函数R(D)的自然推广。我现在称之为语义信息G理论。我于1999年于Int. Journal of General Systems发表了一篇英文长文【9】，它是《广义信息论》的概要和改进版。最近十年，我加强了语义信息论和机器学习相结合的研究，又于《智能系统学报》、Entropy和Information等期刊发表了大约十篇文章(包括三篇综述文章)【8,10-16】。我最近十年的研究进展【11】包括：机器学习应用(多标签学习和分类，最大互信息分类， 混合模型，主动推断或约束控制，求解隐含变量)，贝叶斯确证(包括解决乌鸦悖论)，改进变分贝叶斯和最小自由能原理【12】。由于我最近十年发表的大多是英文文章，国内同行大多只知道我早年研究。本文简要介绍G理论和机器学习应用进展，以便和国内同行交流。

2. 语义信息G理论简介

         2.1. P-T 概率框架和语义信道

一个假设或标签y_j有2种概率：统计概率P(y_j)和逻辑概率T(y_j)。统计概率是归一化的(相加等于1)，而逻辑概率不是归一化的。比如y表示3个可能的标签中的一个：y₁=“非成年人”， y₂=“成年人”，y₃=“年轻人”。3个标签被选择的概率(统计概率)之和是1，但是它们为真的概率(逻辑概率)之和大于1——因为y₁和y₂的逻辑概率之和就等于1。

条件逻辑概率就是真值T(y_j|x_i). 设y_j=“x在模糊集合θ_j 中”，y_j的真值函数T(y_j|x)也就是θj 是隶属函数，即T(y_j|x)=T(θ_j|x). 真值函数贝叶斯定理可以推广到逻辑概率，即：

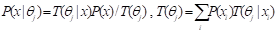                   (1)

式中P(x|θ_j)是似然函数。假设隶属函数的最大值是1，从P(x)和P(x|θ_j)也能得到隶属函数：

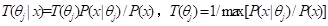          (2)

一组转移概率函数构成一个香农信道，一组真值函数构成一个语义信道。当后者匹配前者时， 即T(θ_j|x)∝P(y_j|x) (j=1,2,…)，有P(x|θ_j) = P(x|y_j) (j=1,2,…)，这时语义信息量达到最大。

真值函数和失真函数d(x,y_j)之间可以通过下式相互转换【11】：  

T(y_j|x) ≡ exp[–d(x, y_j)],  d(x, y_j) ≡ –logT(y_j|x).                   (3)

       2.2 兼容Popper思想的语义信息测度

语义信息量公式是

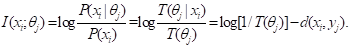      (4)

语义信息公式图解见图1。

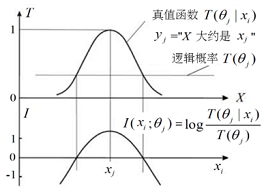
图1 语义信息量公式

它意味着：先验逻辑概率越小，后验逻辑概率越大，语义信息量越大；如果偏差过大，语义信息量是负的。它符合Popper思想。当隶属函数总是1或失真总是0的时候，上面语义信息公式就变成Carnap和Bar-Hillel的语义信息公式。

I(x_i; θ_j)也可谓为y_j反映x_i的逼真度。对I(x_i; θ_j)求平均，就得到语义Kullback-Leibler (KL)信息I(X; θ_j)和语义互信息I(X; Y_θ) ：

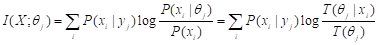      (5)

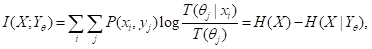        (6)

当P(x|θ_j)=P(x|y_j)(j=1,2,…)时，语义互信息就变成香农互信息。H(X|Y_θ)就是变分贝叶斯(VB)【17】和最小自由能原理(FEP)【18,19】中的变分自由能F，即F= H(X|Y_θ) 【12】。从式(3)可以看出，最大语义信息准则等价于最小交叉熵准则和最大似然准则，也等价于最小变分自由能准则。

2.3 信息率逼真函数R(G)和语义变分贝叶斯

推广信息论失真函数R(D)，即用I(x_i; θ_j)代替失真d(x_i, y_j)，并用语义互信息下限G代替平均失真上限D，就得到信息率逼真函数R(G)。给定信源P(x)，最小化香农互信息所需要的香农信道可以通过迭代方法(重复下面两个公式)求出：

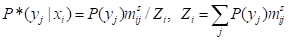，              (7)

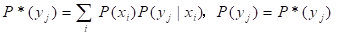，                  (8)

其中m_ij=P(x_i|θ_j)/P(x_i)=T(θ_j|x_i)/T(θ_j), Z_i是分子之和或划分函数。

所有R(G)函数都是碗状的(见图3)，并且其中有个重要的点：s=dR/dG=1，R=G。表示在这一点语义信道匹配香农信道，信息效率r=G/R最大，为1。关于R(G)的更多讨论见文献[31]。

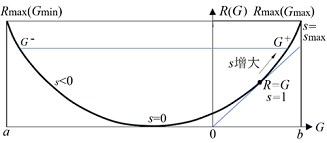
图2. 信息率逼真函数R(G)——给定语义互信息G时的最小香农互信息R

    根据最大似然、最大语义信息或最小变分自由能准则，我们可以从公式(5)得到优化的P(x|θ_j)或T(θ_j|x)。用最小互香农信息准则，从公式(7)和(8)得到优化的香农信道P(y|x). 两种优化方法合并一起就成为语义变分贝叶斯(SVB)【12】。和变分贝叶斯(VB)不同, 其运算简单，约束函数不限于似然函数——也可以是真值、隶属、相似或失真函数。

3. G理论应用

3.1 多标签学习和分类

从样本{(x_k, y_k), k=1,2,…,N}, 我们能得到样本分布P(x, y)。然后用公式(2)或(5)得到优化的真值函数(即语义信道匹配香农信道)。然后用最大语义信息准则得到分类函数(即香农信道匹配语义信道)：

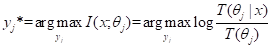，                   (9)

流行的二元关联法(Binary Relevance)把一个n标签学习任务转换为n对标签的学习任务。与之相比，上面方法要简单得多。

3.2 最大互信息分类

假设样本分布是P(x, z)，x是真类别，z是特征矢量，y是根据z预测的类别，我们根据z预测y, 使得香农互信息I(X; Y)达最大。设z的论域是W, S是W的一个划分，到z落入子集C_j，我们预测x是y_j。最大互信息分类就是求：

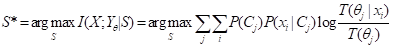.   (10)

求解方法是，先假定一个划分S, 然后重复下面两个步骤，直至S收敛到S*：

1）  令语义信道匹配香农信道：即求出P(y_j|x), I(x; θ_j)和I(X; θ_j|z), (j=1,2,…);

2）  令香农信道匹配语义信道：即令。

这种分类方法对低维特征空间尤为合适。

3.3 混合模型收敛证明

EM算法通常用于混合模型和聚类——一种无监督学习方法。我们知道P(x)=∑_j P(y_j)P(x|y_j)。给定样本分布P(x), 我们使用P_θ(x)=∑_j P(y_j)P(x|θ_j)逼近 P(x), 使得相对熵 H(P‖P_θ) 接近 0。 我把EM算法改进为EnM算法。E-step不变，M-step只更新似然函数，n-step重复等式(7)和(8)n次。我推导出公式：

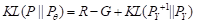.                                               (11)

M-step最大化G, E-step最小化R，n-step最小化KL(P||P_θ)， 所以EnM和EM算法收敛.同时我证明了：流行的看法——认为EM算法收敛过程中，完全数据对数似然度Q不断增大。这是不对的，参看我提供的反例【12】。

3.4 贝叶斯确证

       确证或贝叶斯确证是归纳的现代形式——在评价规律或大前提的时候，用确证度代替真假判断。确证理论的难题在于：1)存在确证悖论或乌鸦悖论。根据经典的逻辑理论，大前提“yàx”(即“若y则x”)和“非xà非y” 等价，所以，“乌鸦是黑的”(H₁)和“不黑的不是乌鸦”(H₂)等价。据此，一根白粉笔或白猫支持后H₂, 从而也支持H₁. 但是按照常识，黑乌鸦支持H₁，不黑的乌鸦否定H₁，非乌鸦物体，比如白粉笔和H₁不相关。所以，在常识和经典逻辑之间存在悖论。2)确证度要和医学检验理论兼容。

         为此，我区分信道的确证(评价规则有多好)和预测的确证(评价结果x有多可靠)【13】。我用最大语义信息准则推导出两个确证测度b*和c*, b*反映规则有多好，和医学检验理论兼容：c*反映后件x有多可靠，能用于澄清乌鸦悖论。

         两种确证测度都强调较少的反例比较多的正例更加重要，从而兼容Popper的证伪理论。

3.5 用于数据压缩和主动推断

         经典的数据压缩理论使用信息率失真函数，它用最小平均失真准则；而G理论使用最信息率逼真函数R(G). 除了准则不同(改变失真准则为语义信息准则)，约束也更加多样化。比如可以用真值、隶属或相似函数或语义信道T(y|x)表示约束范围【12】。

       Friston等人发展出主动推断，我提出约束控制(使用目标定向信息或合目的信息准则)，两者任务类似。它们都和数据压缩密切相关。不同的是：对于数据压缩， 信源P(x)不变，误差在预测y和事实x之间；而对于主动推断，P(x)变为P_θ(x), 误差在理想和现实之间，即在P(x|θ_j)和P(x|y_j)之间或在T( θ_j|x)和P(y_j|x)之间。我提出的语义变分贝叶斯解决这些问题更加简单【12】。

3.6 投资组合和信息价值

         美国诺贝尔获奖者Arrow曾以投资组合为例，结合香农熵讨论了信息价值，美国著名信息论教科书【20】作者Cover结合投资组合和香农互信息讨论了信息价值。我结合投资组合和语义互信息讨论了信息价值。Arrow和Cover得出1比特信息带来翻倍收益的结论。我的分析否定了他们的结论，认为他们的分析有错，信息价值应该和赔率有关【11】。

         我还改进了Kelley打赌公式，得到更一般结论。比如对于掷硬币打赌，最优投资比例是

q*=E/(r₁r₂).                                                       (12)

其中E是期望收益， r₁和r₂分别是盈利和亏损倍数。比如对于赚40%亏30%等可能的打赌，期望收益是0.05，q*=0.05/(0.3*04)≈0.42.

       另外，我还证明了分散投资极限定理(对于掷硬币打赌，随着分散投资数目n增大，几何平均收益将接近算数平均收益)，提出新的风险测度，得到投资容量公式：

。                                          (13)

它和高斯信道容量公式非常相像——风险相当于噪声。

4. 最新动向——挑战和改进最小自由能原理

    我在【12】种指出：变分贝叶斯(VB)和最小自由能原理(FEP)存在三个缺点：1)变分自由能在优化过程中并不总是减小的，对于混合模型，存在反例；2)变分自由能概念和物理学自由能概念有冲突；3)约束条件仅限于似然函数。为此，我提出语义变分贝叶斯和最大信息效率原理，用以克服这三个缺点。语义变分贝叶斯和最大信息效率原理容易理解，计算也更加简单【12】。

Friston等人【17,18】用FEP解释生物对环境的感知和适应(包括干预)，促进自组织和有序。相对最大熵原理，这是一大进步。最大信息效率原理应能更好解释和促进生物自组织。

5.  总结

语义信息G理论是香农信息论的自然推广， 就像交叉熵是香农熵的自然推广。除了使用交叉熵，它还使用P-T概率框架，从而建立真、失真(涉及逻辑概率)和统计概率之间的联系。其解决问题的能力已经在机器学习和科学哲学的应用中得到体现。

其未来发展方向包括：

1）  倡导在优化语义通信和数据压缩时用最大互信息或最小变分自由能准则代替平均失真准则；这等于用最小残差编码长度优化概率预测，更加符合香农基本思想。

2）  结合深度学习发展语义信息论。语义变分贝叶斯已经显示它在无监督学习领域的理论优势，但是如何用语义信息G理论解释和改进word2vec，还需要进一步探讨。

3）  把最大信息效率原理应用到生物学领域，它应能比最小自由能原理更好解释生物自组织和地球的有序。

6. 参考文献

【1】Claude E. Shannon, Warren Weaver. The Mathematical Theory of Communication, The University of Illinois Press: Urbana, IL, USA, 1963.

【2】Rudolf Carnap, Yehoshua Bar-Hillel. An Outline of a Theory of Semantic Information; Tech. Rep. No. 247; Research Laboratory of Electronics, MIT: Cambridge, MA, USA, 1952.

【3】Fred I.Dretske. Knowledge and the Flow of Information, Cambridge, Massachusetts The MIT Press, 1981.

【4】钟义信. A Theory of Semantic Information. Proceedings 2017, 1, 129.

【5】鲁晨光，广义信息论，中国科技大学出版社，1993.

【6】Luciano  Floridi. Outline of a theory of strongly semantic information. Minds and Machines, 2004, 14, 197-221. 

【7】马克.布尔金. 信息论——本质.多样性.统一，知识产权出版社：北京，2015.

【8】鲁晨光，A Semantic Generalization of Shannon’s Information Theory and Applications，Entropy 2025, 27(5), 461.

【9】鲁晨光. A generalization of Shannon’s information theory. Int. J. Gen. Syst. 1999, 28, 453–490.

【10】鲁晨光. The P–T probability framework for semantic communication, falsification, confirmation, and Bayesian reasoning. Philosophies 2020, 5, 25.

【11】鲁晨光 Semantic Information G Theory and Logical Bayesian Inference for Machine Learning. Information, 2019, 10, 261.

【12】鲁晨光，Improving the Minimum Free Energy Principle to the Maximum Information Efficiency Principle，Entropy 2025, 27(7), 684.

【13】鲁晨光. Channels’ confirmation and predictions’ confirmation: From the medical test to the raven paradox. Entropy 2020, 22, 384.

【14】鲁晨光. The P–T probability framework for semantic communication, falsification, confirmation, and Bayesian reasoning. Philosophies 2020, 5, 25.

【15】鲁晨光. Reviewing evolution of learning functions and semantic information measures for understanding deep learning. Entropy 2023, 25, 802.

【16】汪培庄，鲁晨光.从随机集落影到随机点落影——隶属函数用于机器学习，智能系统学报，2025年，卷20，第2期，第305-315页.

【17】Geoffrey E. Hinton and Drew van Camp. Keeping the neural networks simple by minimizing the description length of the weights. In Proceedings of COLT, pp. 5–13, 1993.

【18】Karl J. Friston. The free-energy principle: a unified brain theory?. Nat Rev Neurosci 2010, 11, 127–138.

【19】Maxwell J. D. Ramstead，Paul. B. Badcock,  Karl J. Friston . Answering Schrödinger's question: A free-energy formulation. Phys Life Rev. 2018 24, 1-16.

【20】Thomas M. Cover, Joy A. Thomas. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 2006.